[Featured Image credits to CaitlinJo, CC BY 3.0 (http://creativecommons.org/licenses/by/3.0), via Wikimedia Commons: commons.wikimedia.org/wiki/File:Pi_30K.gif
O método de Monte Carlo (MC), desenvolvido em meados do séc. XX, constitui uma das técnicas de simulação computacional mais utilizadas. Uma simulação por MC visa determinar soluções via análise estocástica recorrendo ao conceito de número aleatório, de modo a que se possa descrever (probabilisticamente) o comportamento de um dado sistema e calcular variáveis de interesse para análise do mesmo. OK…vamos desencriptar isto.
MC recorre ao conceito de número aleatório. Um número aleatório é um número que é escolhido ao acaso. Pode exemplificar-se recorrendo a um dado: quando lançamos um dado obtém-se um número de 1 a 6, mas à partida não sabemos que número sairá visto que cada um tem igual probabilidade de saída. Esta imprevisibilidade de saída determina a aleatoriedade. Se lançarmos o dado várias vezes e formos anotando os números que forem saindo obtemos uma sequência de números aleatórios. Se esta sequência for verdadeiramente aleatória não temos forma de nela decifrar algum padrão que permita a prever o número que se segue. Existem algoritmos computacionais que geram sequências ‘quase’ aleatórias, diz-se quase porque os algoritmos são na realidade deterministas, dependendo das condições iniciais e, em particular, da chamada seed (semente). Estes geradores de números aleatórios designam-se pseudo-aleatórios.
E isto é importante porquê? A implementação de MC passa pela geração de uma sequência de números aleatórios. Vamos aqui apenas requerer que a sequência seja aleatória “o suficiente” para que permita gerar uma distribuição de números uniforme. Tente-se um exemplo….o exemplo canónico simples muitas vezes apresentado quando se fala deste tópico: calcular o valor aproximado de pi. Imaginemos que se quer determinar o valor de π (pi).
Sabemos que a área de uma circunferência de raio r é dada pela expressão π r2. Sabemos ainda que a área de um quadrado de lado l é dado por l2. Se circunscrevermos uma circunferência de raio r num quadrado (de lado 2r), podemos usar MC para saber a relação entre as área das duas figuras geométricas. Vamos desenhar um quadrado e circunscrever uma circunferência, fazendo 2r=l=1m. Experimentemos mesmo desenhá-lo no chão, e em seguida, vamos atirar pedrinhas (todas iguais) para dentro da área do quadrado (nada pode cair fora), e tente-se que ao atirar se distribuem as pedrinhas uniformemente pela área do quadrado. Após atirarmos pedrinhas suficientes (muitas!) contam-se as pedrinhas que cairam dentro da circunferência e as que ficam de fora ou seja todas as pedrinhas, para saber o número total (contamos todas as que estão dentro do quadrado).
A relação entre o número de pedrinhas é igual á relação entre as áreas, e assim podemos saber o valor aproximado de π. Vejamos:
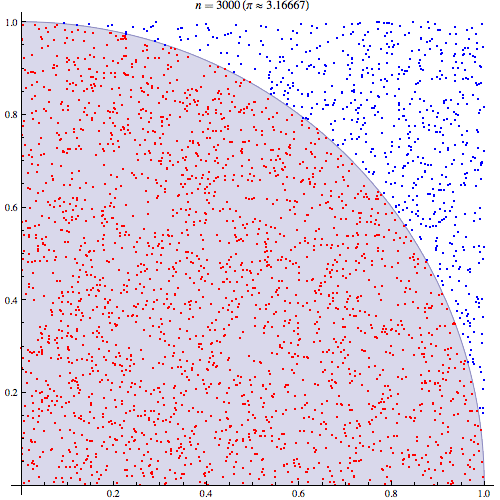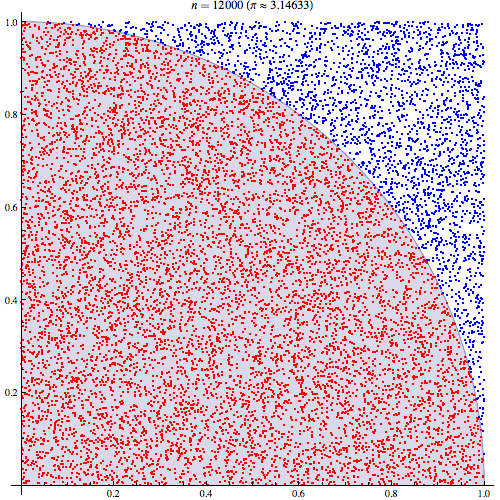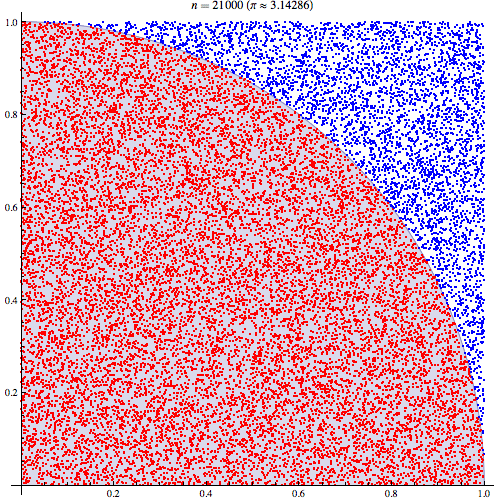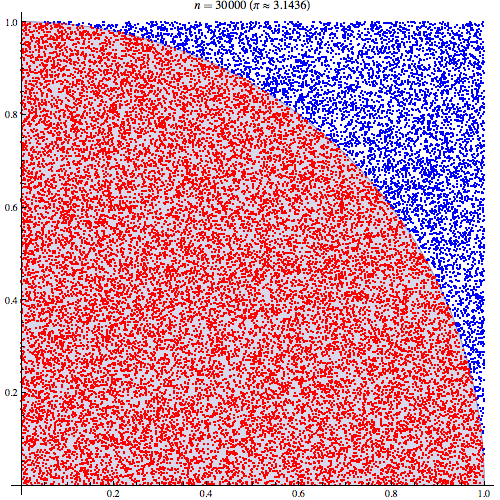
Observe-se a imagem animada no início do artigo. Experimente repetir atirando o dobro das pedrinhas….e, novamente, agora com metade das pedrinhas. O que observa?
A ilustração permite-nos ter uma ideia: quanto mais densa for a distribuição de pedrinhas melhor será a aproximação ao valor de π. Agora tente atirar as pedrinhas sem o ‘cuidado’ de as distribuir uniformemente. Ou imagine apenas que, no caso limite, o mesmo número de pedrinhas ao serem atiradas caiem todas na área da circunferência. Concluir-se-ia que a área do quadrado é igual à área da circunferência, o que constitui uma aproximação bastante grosseira à área de um quadrado e, consequentemente, ao valor de π, neste caso sai directamente π = 4.
Concluímos então que a distribuição de pedrinhas tem que ser o mais uniforme possível, cada ‘atirar uma pedrinha’não pode ou correlacionada com nenhum outro ‘atirar uma pedrinha’…o mais aleatória possível. Então parece que o mais complicado é conseguir arranjar um gerador de números aleatéorios que seja suficientemente bom para permitir melhor exactidão nos resultados.
Na realidade o problema da amostragem de números e sequências aleatórias é central em MC. Como em geral precisamos de muitas (muitas muitas…) pedrinhas se calhar não encontraríamos pedrinhas (nem tempo!) suficientes para nos focarmos no essencial da questão. Como tal, usamos um simples computador, aproveitamo-nos da sua incrível rapidez e capacidade de não se aborrecer ao ter que fazer milhares de contas ‘iguais’ e, recorrendo à nossa linguagem de programação preferida, escrevemos um pequeno programinha.
Para o exemplo acima, usando a linguagem de programação C, podemos escrever:
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
main() {
int i, count =0, Nit = 0;
double x, y, dist, pi;
printf ("Escreva o numero de iterações a resolver para calcular pi: ");
scanf ("%d",&Nit);
/* Inicializar o gerador de números aleatórios */
srand (time(NULL));
count = 0;
for (i = 0; i < Nit; i++) {
x = (double) rand () / RAND_MAX; /*gera um numero aleatorio entre 0 e 1 */
y = (double) rand () / RAND_MAX;
dist = x * x + y * y;
if (dist <= 1) count++; /* Caiu dentro da circunfrencia? Entao somar 1 */
}
pi = (double) 4 * count / Nit; /* Calcular pi*/
printf ("Para uma amostragem de %d números aleatórios:n %d pontos cairam dentro da 'area circunfrencia. O valor de pi e' %g. n", Nit, count, pi);
}
Gravamos num ficheiro, calcpi.c. Agora é só compilar na shell (ambiente linux)
gcc calcpi.c -o calcpi
E chamar o programa
./calcpi
Depois é fazer uns testes….note-se que é muito mais rápido que atirar e contar pedrinhas 😉 No programinha acima confiamos que a função interna da biblioteca math.h – rand() permite-nos obter uma distribuição uniforme de números aleatórios. Cada chamada de rand() devolve um número pseudo aleatório entre 0 e RAND_MAX (no mínimo 32767). A função srand() inicializa o gerador de números aleatórios com a seed (semente) que é dada como argumento, no nosso exemplo é usada a função time() que devolve um valor calculado com base na hora actual.
Semelhante raciocínio pode ser utilizado se quisermos utilizar o método para calcular o integral definido I de uma função f(x), no intervalo [a, b].
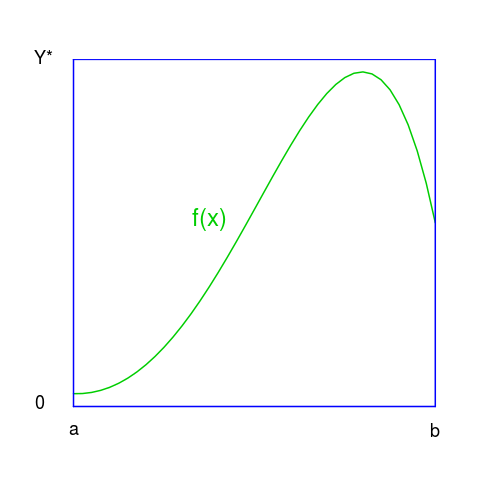 Analogamente ao caso anterior, podemos aproximar o valor do integral atirando pedrinhas para o rectangulo de lados (AB) e (0Y*). E procedendo de modo semelhante na contagem.
Analogamente ao caso anterior, podemos aproximar o valor do integral atirando pedrinhas para o rectangulo de lados (AB) e (0Y*). E procedendo de modo semelhante na contagem.
Neste caso a condição a verificar para a contagem de Nf consiste em saber se o número aleatório gerado (y = rand()) é menor (ou igual) que o valor da função num ponto (x = rand()) também gerado aleatoriamente: if y <= f(x) then count ++. Concluímos que a exactidão do método depende:
- do número de pedrinhas — número de iterações. O erro da simulação de MC é proporcional a 1/sqrt(N), sendo N o número de iterações, e N grande ;
- da aleatoriedade na distribuição das pedrinhas. É suficientemente uniforme? Não correlacionada? Se possível sem repetições. — qualidade do gerador de números aleatórios em gerar uma distribuição uniforme, não correlacionada, e de período longo.
Repare-se que nos exemplos acima todos os pontos da área do rectângulo têm a mesma importância, cada um contribui com o mesmo peso para o cálculo do integral. Por vezes é útil efectuar uma amostragem mais ‘refinada’ em certas zonas da função que queremos integrar. Por exemplo em zonas onde a função varia mais rapidamente, onde esta é mais ‘importante’. A este processo chama-se importance sampling. Num proximo post escreverei acerca de um caso particular em que o importance sampling é utilizado – a Regra Metropolis.
Referências:
Outras…
- Metropolis, N. (1987). “The beginning of the Monte Carlo method”, Los Alamos Science, Special Issue 15: 125-130 . (PDF)
- Anderson, Herbert L. (1986). “Metropolis, Monte Carlo and the MANIAC” Los Alamos Science 14: 96–108. (PDF)
- Eckhardt, Roger (1987). “Stan Ulam, John von Neumann, and the Monte Carlo method” Los Alamos Science, Special Issue 15: 131–137. (PDF)
- R: https://www.r-project.org/; (Wikipedia link)
Para desenhar a figura acima recorreu-se a programação em R
png("plotMC.png")
x <- seq(from = 0, to = 4, by = 0.1)
plot(x, -.2*x^5 -.4*x^4 +2*x^3 + 15*x^2 - x + 12,type='l', ylab = " ",xlab = ' ', col='green3', axes = F, frame.plot=F, lwd =2 )
segments(0, 123.05, 4, 123.05, col = 'blue', lwd = 2)
segments(0,7.75, 4, 7.75, col = 'blue', lwd = 2)
abline(v=4, col = 'blue', lwd = 2)
abline(v=0, col = 'blue', lwd = 2)
text(x=c(0:4),0, labels =c('a',' ', ' ',' ', 'b'), xpd = T, , cex = 1.5)
text(x = 0, 7, labels =c('0'), adj = c(3.85,0) , xpd = T, , cex = 1.5)
text(x = 0, 121.5, labels =c('Y*'), adj = c(2.1,0) , xpd = T, cex = 1.5)
text(x = 1.5, 70, labels =c('f(x)'), cex = 2, col = 'green3')
dev.off()
Muito obrigado por esta publicação. Foi muito util.
Jorge Matos, obrigada!