MC e a Regra Metropolis

_{Featured image: , by Leonardo Casto, icensed under the Creative Commons Attribution-Share Alike 2.5 Generic license.}

Viva, já revi um pouco o texto 🙂 aqui está de novo.

Num post anterior fez-se uma pequena introdução ao método Monte Carlo. Aqui a ideia é introduzir os conceitos de importance sampling, detailed balance e apresentar a regra  Metropolis, num contexto emque se pretende calcular a/uma configuração de equilíbrio de um sistema.

Dependendo da dimensão do sistema em estudo, calcular aleatoriamente a energia de cada configuração do mesmo pode ser impraticável. O ideal seria então conseguir reduzir a computação a um conjunto de configurações que mais nos interesse. Assim, o problema passaria por construir uma amostra pesada cuja distribuição de estados seja dada pela distribuição de probabilidade do equilíbrio. Como o fazer?

Mas…mais devagar…

1. Importance Sampling e Detailed Balance

A probabilidade de transição de um estado a outro, \displaystyle W(x \to x') , adequada, obedece às seguintes características:

1. \displaystyle \text{ergodicidade, } W(x \to x') \neq 0;

2. \displaystyle \text{positividade, } W(x \to x') \geq 0;

3. \displaystyle \text{normalizada (ou normaliz\'avel), }\sum_{x'} W(x \to x') = 1;

4. \displaystyle \sum_{x'} W(x' \to x) P (x' , t) = P (x , t),  \text{ considerando } P(x, t)   \displaystyle \text{ a probabilidade de, no instante }  t\text{, o estado }  x \text{ ocorra.}

Voltando ao referido anteriormente, a ideia subjacente ao importance sampling consiste em efectuar uma amostragem de uma distribuição não uniforme, considerando uma função de distribuição de probabilidade cujo comportamento seja o mais semelhante à função sobre a qual vai ser aplicado o MC. Ou seja, respeitar a distribuição das configurações do sistema e dar maior ênfase às que mais contribuem para o integral – às que correspondem a um maior valor de \displaystyle P(x). Note-se que, deste modo, é possível reduzir a variância do estimador MC.

As probabilidades de transição, ou probabilidade de o sistema transitar do estado onde se encontra para um novo estado, determinam a construção da chamada cadeia de Markov. Uma cadeia de Markov é uma sequência de números aleatórios construída de forma tal que a probabilidade de um determinado valor ocorrer depende apenas do número que ocorreu previamente, ou de outro modo a probabilidade de transição para o estado seguinte depende apenas do estado presente. Diz-se então que a probabilidade está condicionada pelo estado imediatamente anterior, ou ainda que o processo “não guarda (ou não tem) memória” de estados passados.

Assim, pode  construir-se um passeio aleatório (uma sucessão de passos aleatórios) [sobre passeios aleatórios ver [1]] tendo em conta a distribuição de probabilidade \displaystyle P(x) , a definição da probabilidade de transição  \displaystyle W(x \to x') e o conceito de importance sampling.

A evolução de  \displaystyle P(x, t) no tempo fica descrita pela equação cinética Markoviana:

\displaystyle \frac{d}{dt}P(x, t) =\sum_{x'} W(x'\to x) P(x', t) - \sum_{x'} W(x \to x') P(x, t)

No equilíbrio termodinâmico tem-se,

\displaystyle \frac{d}{dt}P(x, t) = 0

e consequentemente a probabilidade de transição deverá satisfazer

\displaystyle W(x'\to x) P(x', t) = W(x \to x') P(x, t) . Esta não é nada mais que a condição de detailed balance.

A condição de detailed balance diz-nos que a probabilidade de transição depende exclusivamente da diferença de energia entre os dois estados em causa – permite a reversibilidade de cada transição.

Como \displaystyle P(x, t) = P_{eq}(x) = Z^{-1}e^{-\beta\Delta H(x)}, sendo \displaystyle Z a função de partição, a condição de detailed balance pode reescrever-se:

\displaystyle \frac{W(x \to x')}{W(x' \to x)} = e^{-\beta\Delta H(x)}, \Delta H(x) = H(x) - H(x')

A propriedade de detailed balance garante a convergência do passeio aleatório para uma distribuição de probabilidade fixa.

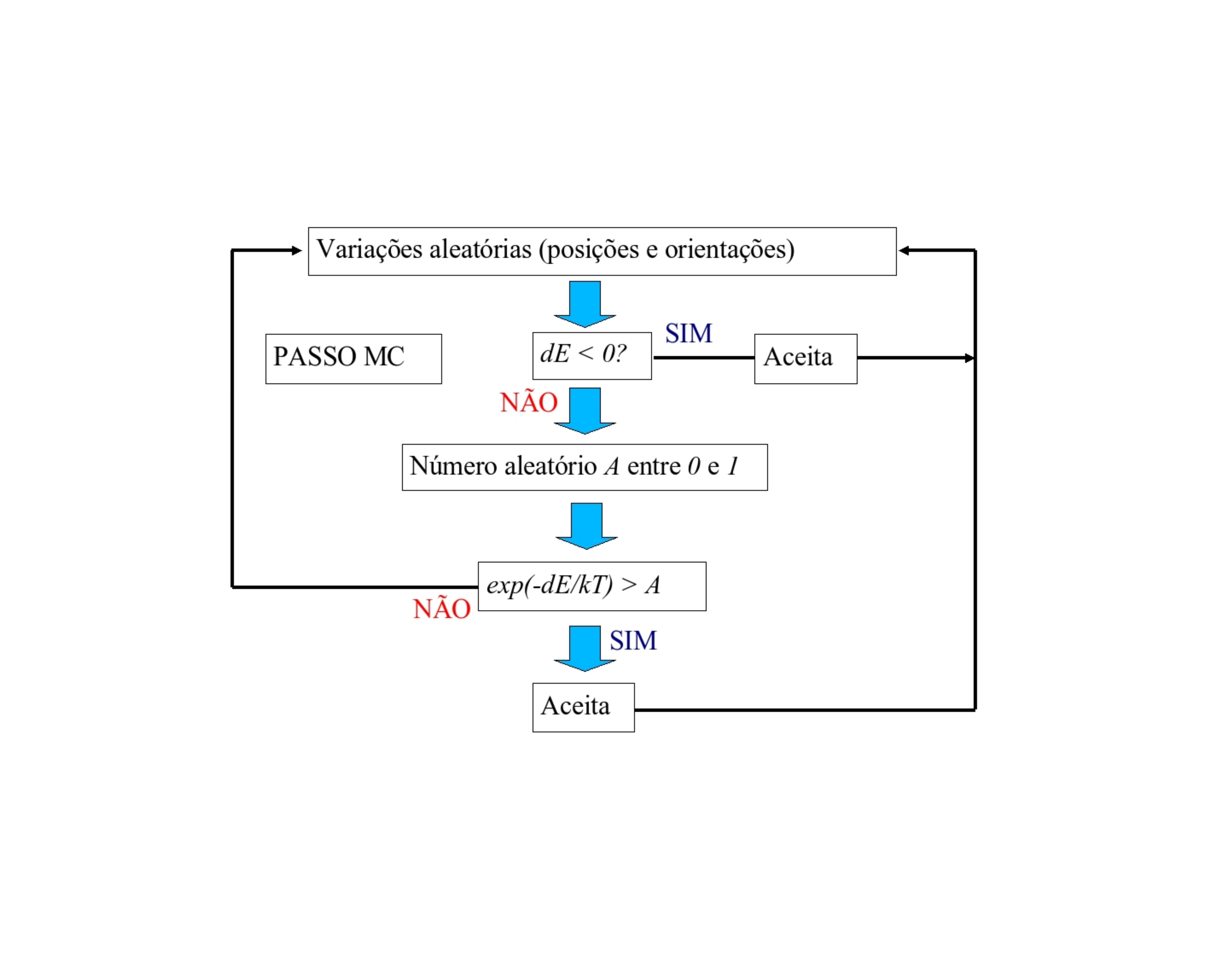
1. A regra Metropolis

A regra Metropolis tem implícita uma amostragem markoviana num sistema em equilíbrio, com uma determinada função de distribuição de probabilidade e definindo como probabilidade de transição o seu quociente, consequência da condição de detailed balance [1]:

\begin{cases} \frac{1}{\tau} e^{(-\beta\Delta H)}& \quad \text{if } \Delta H > 0 \\ \frac{1}{\tau} & \quad \text{if } \Delta H \leq 0\\ \end{cases}

com \tau} em unidades de tempo. Sem perda de generalidade considerou-se \tau} = 1.

A transição é então aceite:

1. incondicionalmente, se a energia diminuir com a transição;

2. no caso de a energia aumentar com a transição, é aceite condicionalmente: se  e^{−Hx},  gerado aleatoriamente no intervalo ]0, 1[.

O método permite rápida convergência para um estado de equilíbrio uma vez que  aceita sempre a melhor configuração. Ao aceitar ocasionalmente configurações menos óptimas, garante-se o não aprisionamento em mínimos locais. Nota: Deve ter-se em atenção à topologia das barreiras, uma transição de estado assim definida pode ainda conduzir à retenção em mínimos locais. Existem variantes do algoritmo de Metropolis que podem ser aplicadas nestes casos.

MC Metropolis pode ser aplicado ao estudo de diversos problemas como o da simulação de cadeias de moléculas, em particular o estudo do problema de folding de proteínas, abordado anteriormente.

Referências:

• [1] Sobre random walks, self-avoiding walks… http://www.americanscientist.org/issues/pub/1998/4/how-to-avoid-yourself
• [2] Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of State Calculations by Fast Computing Machines. The Journal of Chemical Physics 21, 1087–1092 (1953). (AIP)(PDF)

Outras…

• Metropolis, N. (1987). “The beginning of the Monte Carlo method”, Los Alamos Science, Special Issue 15: 125-130 . (PDF)
• Anderson, Herbert L. (1986). “Metropolis, Monte Carlo and the MANIAC” Los Alamos Science 14: 96–108. (PDF)
• Eckhardt, Roger (1987). “Stan Ulam, John von Neumann, and the Monte Carlo method” Los Alamos Science, Special Issue  15: 131–137. (PDF)
• O mistério da forma das proteínas, Patrícia F.N. Faísca, Gazeta da Física, pp. 34-39,  cftc.cii.fc.ul.pt/divulga/Misterio_gazeta.pdf

Este artigo foi  inspirado num trabalho realizado no âmbito da cadeira de Física Computacional (com o meu colega Rui P.),  (2006).