This article is a version of section 1.6 – Chapter 1, of my doctoral thesis, Functional MRI of stimulus interference on auditory processing in normal listeners and tinnitus patients available @ http://hdl.handle.net/10362/14989, (minor wording modifications were applied).
Professor Bloch has told you how one can detect the precession of the magnetic nuclei in a drop of water. Commonplace as such experiments have become in our laboratories, I have not yet lost a feeling of wonder, and of delight, that this delicate motion should reside in all the ordinary things around us, revealing itself only to him who looks for it.
E. M. Purcell – Nobel Lecture: Research in Nuclear Magnetism (Purcell, 1953).
fMRI is a technique that allows the production of images of the human brain, and identify which regions are active as response to stimulus variations or presentations. It is a considerably safe technique, and since it is non-invasive it became a privileged way to study the human brain. It has good spatial resolution of the order of millimeters, however the nature of the signal that it is measured limits the temporal resolution to the order of seconds.
MRI physics: the spin, the magnetic field and the radio frequency coils
MRI physics is based on the concept of nuclear magnetic resonance (NMR) first described in 1946 by Felix Bloch (Bloch, 1946; Bloch et al., 1946), by Edward Purcell (Purcell et al., 1946), and their respective colleagues. To have NMR we need a non-zero spin atomic nuclei (Nuclear), a strong magnetic field (Magnetic), and a radio frequency coil (Resonance).
The spin
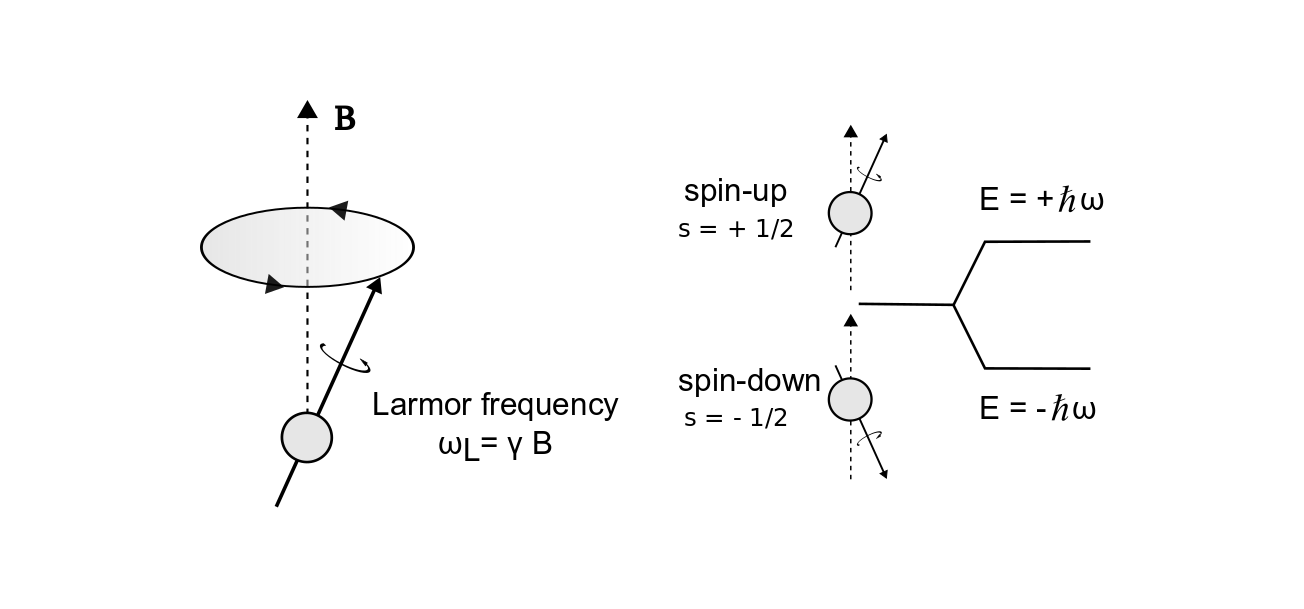
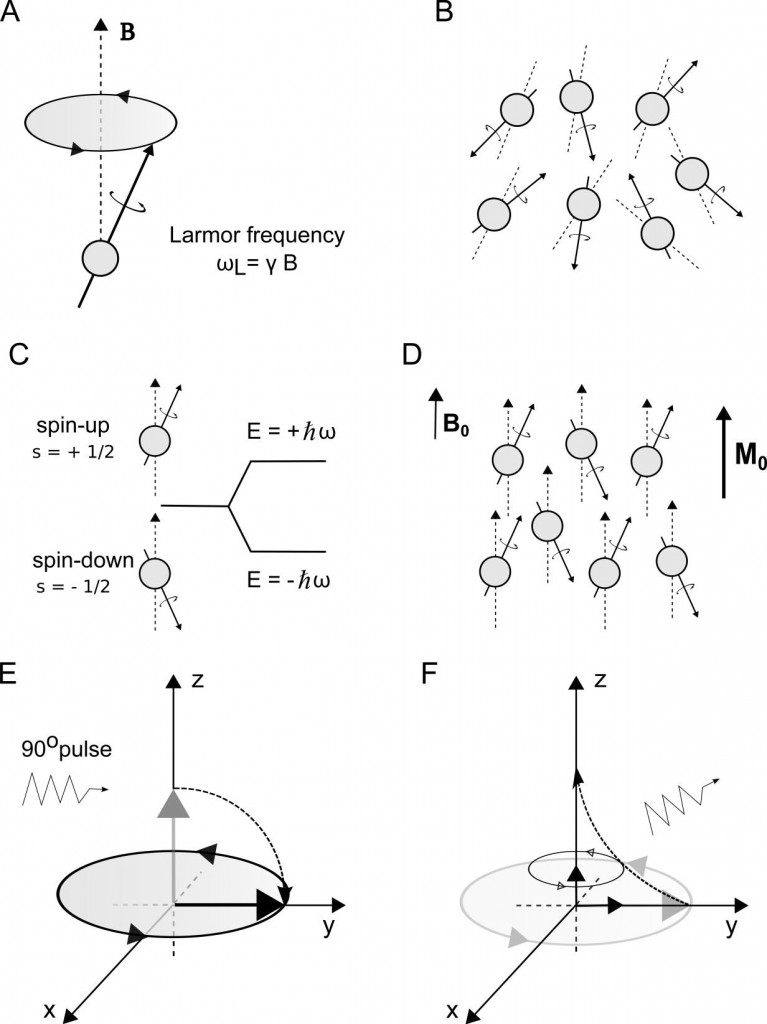
‘Spin’ is a property of some particles that causes the nuclei to possess a magnetic moment and an angular momentum. Because the nuclei have angular momentum, they will experience an effect called precession, a motion analogous to a spinning top. Precession consists of a circular movement of the rotation axis of the spin, about a second axis of an existing external field (e.g. a magnetic field B), causing the spin axis to change its direction. (Figure 1-A)
Our body is made of different tissues, and all tissues contain water molecules. One water molecule consists of one oxygen and two hydrogen atoms. 16-oxygen and 18-oxygen nuclei do not possess magnetic moment, thus do not interact with an existing magnetic field. However, 17-oxygen does have a magnetic moment, but its abundance in the human body is very low when compared to hydrogen (Haacke et al., 1999). Consisting of a single proton, each of the hydrogen nucleus has a magnetic moment associated to its spin. This means an enormous amount of hydrogen nuclei in our body are spinning, making this a good candidate nucleus to study, using NMR. (Figure 1-B)
The magnetic field B0
In the case of MRI, a strong superconducting magnet is used to create the strong magnetic field B0 to cause the nuclei to precess in turn of a known direction.
In the presence of an external magnetic field, the nuclei will precess in turn of the applied field. Because the proton has only two energy states, the nuclei will tend to align with the external field in a parallel or anti-parallel way – the two important states called spin-up or spin-down, low and high energy states respectively. (Figure 1-C) At room temperature the low and high precessing states are more or less balanced, however there will be a slightly higher proportion of nuclei in low than high. As a result, a tiny majority of spins will tend to align in the lower energy state thereby creating a net magnetization (M0) of all the nuclei in the direction of the main magnetic field, B0. (Figure 1-D)
The net magnetization can be considered in terms of one big spin, and it constitutes the basis of the imaged signal. The behavior of individual spins can only be described by quantum mechanical equations, however a classical description is suitable for the net magnetization vector behavior.
It is necessary to reorient the nuclei out of alignment with B0, and consequently the net magnetization so that the precession can be observed. As the nuclei then fall back in alignment with the main magnetic field, they will release signals that the MRI can detect. In order to reorient the nuclei and to detect the released signal radio frequency coils (RF) are needed.
The radio frequency (RF) coils
Radio frequency coils are used to produce an electromagnetic field (the RF pulse). This pulse has to be applied perpendicular to the field B0 for the magnetization vector to be deviated from its initial alignment with B0. The RF coils can also be used to receive the signal that is transmitted back from the sample.
The RF pulse is applied at the Larmor frequency of the particle, which in the case of the hydrogen nucleus with one proton and an applied external field of 3T is ∼128 MHz. This will be the required frequency of the applied RF pulse for the proton to resonate (resonance frequency) and allow an energy state transition. If the pulse is applied for long enough the net magnetization vector is flipped out of the longitudinal plane into the transverse plane and a 90° RF pulse (excitation) is said to have been applied. (Figure 1-E) Next, what it is needed in NMR imaging is to reorient the net magnetization vector to its natural state of precession. Therefore, the RF pulse is turned off and a signal can be detected by the RF receiver coil.
In time the spin will experience a returning to the alignment with the B0, and the longitudinal magnetization (M||) component will grow back to equilibrium. This process is called longitudinal relaxation and involves spin-lattice interactions – energy exchange of the spin with the lattice. The growth rate of M|| is characterized by the time constant T1, which for the case of brain tissue is in the order of 1 s. However, not all the protons are bound in their molecules in the same way. This is different for each tissue. T1 depends on the applied magnetic field strength (the longer for stronger magnetic fields).
However, the MRI signal of interest is the signal released by the precession movement of the transverse magnetization during its return to equilibrium. This signal is detected by a receiver coil tuned to the Larmor frequency of the proton. There is the return to equilibrium of the transverse magnetization, M⊥, by a process called spin-spin relaxation. (Figure 1-F)
Each nucleus magnetic field interacts with the other nuclei causing them to precess at a different frequencies (loss of coherence between spins), a process also known as ‘dephasing’ of the spins. (Figure 2)
This results in a signal loss characterized by a time constant T2 (different from the longitudinal relaxation T1). For brain tissue, T2 is in the order of 0.1 s. Additionally, M⊥ decay is caused by variations in local field, or field inhomogeneities that are experienced by the spin nuclei, which affect the transverse relaxation time to a T2* < T2. Therefore, T2* is a combination of T2 dephasing effects and field inhomogeneities. However, by applying an additional RF pulse so that the spins are 180° flipped in the transverse plane, the T2* dephasing can be reversed and the external field dispersion refocused. This is called spin-echo sequence, and the time between the 90° pulse and the spin-echo is known as echo time (TE). The spin-echo process can be repeated several times allowing the acquisition of enough signal so to construct an image. Instead, gradient echo sequences can be used in a process that consists of causing a transverse dephasing and subsequent refocus of the spins. This is achieved with additional coils used to produce a magnetic field that varies in three orthogonal directions – the magnetic field gradients. This also allows the MRI the capacity to image directionally along the three orthogonal axis, which is the basic principle of MRI.
![Dephasing of the nuclei.]{Dephasing of the nuclei. Each nucleus precess at a different frequency causing loss of coherence between the spins.](http://zerpoii.opentronix.com/wp-content/uploads/2015/03/Figure7-precession_LowResolution-1024x522.jpg)
The period of time that exists between successive excitation pulse sequences (two 90° RF pulses) applied to the same slice is called repetition time (TR). TR will determine how much the longitudinal magnetization recovers in this time interval. Various combinations of the parameters can be used to obtain distinct images. Echo-planar imaging (EPI) consisting of a pulse sequence involving multiple dephasing and refocusing gradient-echo sequences can be used to obtain the MRI images. This, consists of the appropriate method for T2* image construction, where the signal decay depends on local field inhomogeneities, which is the property of interest in blood oxygenation level-dependent (BOLD) fMRI.
References
1. Purcell, E. M. Research in nuclear magnetism. Science 118, 431–436 (1953). [Nobel Lecture @ http://www.nobelprize.org/nobel_prizes/physics/laureates/1952/purcell-lecture.html]
2. Bloch, F. Nuclear Induction. Phys. Rev. 70, 460–474 (1946). (APS) (pdf)
3. Bloch, F., Hansen, W. W. & Packard, M. The Nuclear Induction Experiment. Phys. Rev. 70, 474–485 (1946). (APS) (pdf)
4. Purcell, E. M., Torrey, H. C. & Pound, R. V. Resonance Absorption by Nuclear Magnetic Moments in a Solid. Phys. Rev. 69, 37–38 (1946). (APS) (pdf)
5. Haacke, E. M., Brown, R. W., Thompson, M. R. & Venkatesan, R. Magnetic Resonance Imaging: Physical Principles and Sequence Design. (Wiley, 1999).
Additional online resources
The basics of NMR, J.P. Hornak http://www.cis.rit.edu/htbooks/nmr/
License

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.